Non-linear Stability 개요#

강좌: 기초 전산유체역학

%matplotlib inline
from matplotlib import pyplot as plt

import numpy as np

plt.style.use('ggplot')
plt.rcParams['figure.dpi'] = 150

수치 진동#

Odd-Even Decoupling#

Linear wave 방정식에서 다음과 같은 Odd-Even 진동을 해석해보자.

x = np.linspace(0, 6, 7).astype(int)
y = 2*(x % 2) -1

plt.plot(x, y)

[<matplotlib.lines.Line2D at 0xff41d1516b10>]

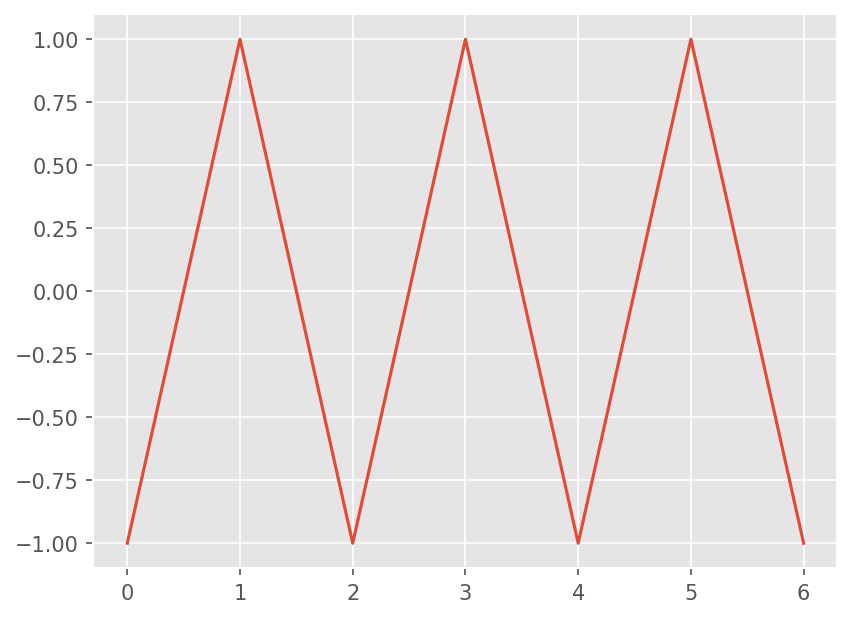
../_images/b47863f6e40eb179bdae4fff8a98bfffc2c56da40bf535c52e8b6895dcb10e66.png

이를 중앙차분법 (Unstable flux)로 계산하면

\[ \frac{\partial u_i}{\partial t} + \frac{a}{2 \Delta x} (u_{i+1} - u_{i-1}) = 0. \]

이 진동은 계속 유지된다.

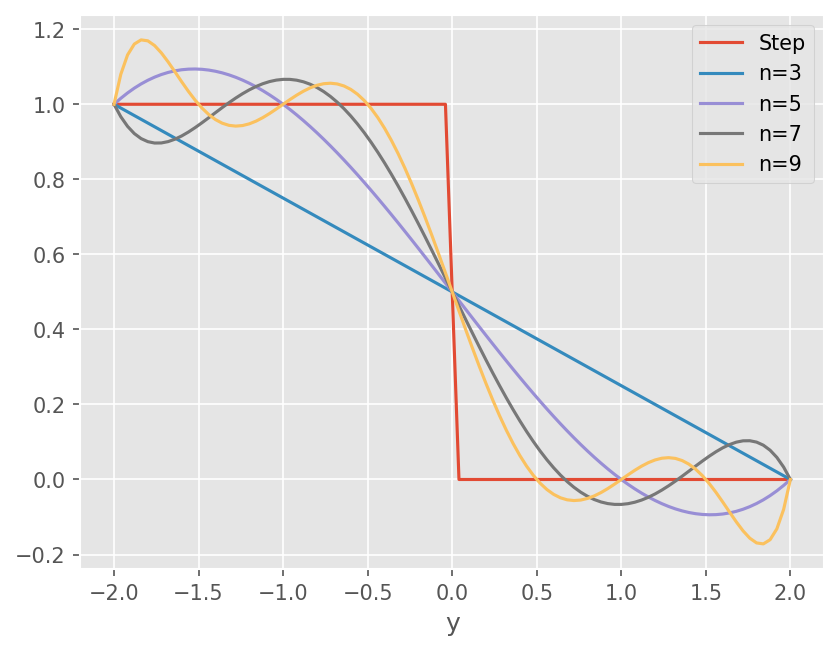
Gibbs oscillations#

불연속 구간을 매우 높은 정확도로 근사할 경우 수치 진동이 발생한다.

x = np.linspace(-2, 2, 101)
stepf = lambda x: (1-np.tanh(1e8*x))/2

fs = []
for n in [3, 5, 7, 9]:
    xdata = np.linspace(-2, 2, n)
    fdata = stepf(xdata)

    f = 0
    for xi, fi in zip(xdata, fdata):
        # Compute Li
        Li = 1
        for xj in xdata:
            if xi != xj:
                Li *= (x- xj)/(xi - xj)

        f += Li*fi

    fs.append(f)
    

plt.plot(x, stepf(x))

for fi in fs:
    plt.plot(x, fi)

plt.xlabel('x')
plt.xlabel('y')
plt.legend([
    'Step', 'n=3', 'n=5', 'n=7', 'n=9'
])

<matplotlib.legend.Legend at 0xff41d14258d0>

../_images/d81b5917eac8717dffd4a1dd741c4f4cf391ee94517410f26782f991e5deb329.png

Monotone scheme#

충격파와 같은 불연속한 해를 안정적으로 해석하기 위해서는 새로운 수치 진동이 발생하지 말아야 한다.
수치 진동이 발생하지 않는, 즉 해의 단조성이 보장되는, 기법을 monotone scheme 이라고 한다.

\[ u_j^0 \geq v_j^0 \rightarrow u_j^n \geq v_j^n \]

Godunov theorem#

(Godunov, 1959) Linear numerical schemes for solving partial differential equations (PDE’s), having the property of not generating new extrema (monotone scheme), can be at most first-order accurate.

Entropy를 만족하는 해#

(Harten et al., 1976) Montone 기법의 경우 Entropy를 만족하는 해로 수렴한다.

실습 (Transonic rarefaction)#

아래와 같이 Burgers 방정식에 대해서 천음속 팽창파를 해석해보자.

\[\begin{split} u_0 (x) = \begin{cases} -0.5~x \leq 0.5 \\ 1.5 \text{ else} \end{cases} \end{split}\]

\(t=0.2\) 일 때 수치 해를 다음 두 기법으로 구하시오.
- Upwind 기법
- Local Lax Friedrich 기법
  
  \[ F_{i+1/2}^n = \frac{1}{2} \left [ f(U_i^n) + f(U_{i+1}^n) \right ] - \frac{1}{2} |a_{i+1/2}| \left ( U_{i+1}^n - U_i^n \right ), a_{i+1/2} = \max(|f'(U_{i}|, |f'(U_{i+1}|) \]

High Resolution Scheme#

비선형 제한자를 도입하여 연속적인 구간에서는 2차 이상의 공간 정확도를 갖고, 충격파 부근에서만 1차 공간 정확도를 갖도록 한다.
충격파 포착 기법 (Shock-capturing method)

\[ F^{HL} = F^{1st} + \phi (F^{High} - F^{1st}) \]

Non-linear Stability 개요

Contents